金山中学2018-2019学年度第一学期高中三年级双周考数学试题
1、填空题
1.已知集合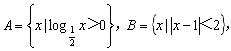
则
_______.
2.若
则关于
的不等式
的解集是________.
3.若圆
与直线
相切,则实数
_______.
4.若
则二项式
的展开式中,
的系数是________.
5.一个四面体的所有棱长都为
且四个顶点在同一球面上,则该球的体积为______.
6.依据射击练习后的统计显示:甲射手射中目的的概率是
乙射手射中目的的概率是
且甲、乙两射手的射击是相互独立的。那样当两人同时射击同一目的时,该目的被射中的概率是__________.
7.某几何体的一条棱长为在该几何体的主视图佛视图左视图中,这条棱的投影长分别
那样_______.
8.在平面直角坐标系
中,角
的顶点在坐标原点,始边在轴的正半轴上,若点P在角
的终边上,点Q
在角的终边上,且
则
______.
9.在等差数列
中,
若此数列的前10项和前18项和
则数列
的前18项和
________.
10.若把椭圆
的长轴AB进行
等分,过每一个等分点作AB的垂线,依次交椭圆的上半部分于点设左焦点为则
_______.
11.设
为
的反函数,则的最大值为_________.
12.在平面直角坐标系中,点之间的“直角距离”为
若
到点A、B的“直角距离”相等,其中实数
满足
则所有满足条件的点C的轨迹的长度之和为_______.
2、选择题
13.双曲线
的实轴长是虚轴长的2倍,则
等于
A. B.
C. D.
14.关于的二元一次方程组其中行列式
为
A.
B. C.
D.
15.若函数
在概念城的某个子区间
上没有反函数,则的取值范围是
A.
B.
C. D.
16.概念:假如一个向量列从第二项起,每一项与它的前一项的差都等于同一个常向量,那样这个向量列叫做等差向量列，这个常向量叫做等差向量列的公差，已知向量列是以
=为首项,公差
的等差向量列，若向量与非零向量
垂直,则
A. B.
C.
D.
3、解答卷
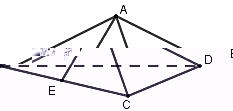
17.如图,在体积为的正三棱锥中,BD=E为棱BC的中点,求:
异面直线AE与CD所成角的大小；
正三棱锥的表面积.
18.已知关于
的方程有两个虚根且满足
求此方程的两虚根及实数的值；
若对于任意
不等式
对于任意
恒成立,求实数的取值范围。
19.因为浓酸泄露对河流形减污染,现决定冋河中投入固体碱,1个单位的固体碱在水中逐步溶化,河流中的浓碱度与时间的关系可近似表示为:
只有当河流中的碱浓度高于1时,才能对污染产生有效的抑制用途。
若只投放1个单位的固体碱,则可以保持有效抑制用途的时间有多长?
当河中的碱浓度开始降低时,即刻第二次投放1个单位的固体碱,此后,每一时刻河中的碱浓度觉得是两次投放的碱在该时刻相应的碱浓度的和,求河中碱浓度可能获得的最大值。
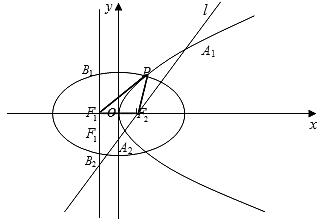
20.如图，设抛物线的准线与轴交于焦点为以为焦点的椭圆
与抛物线在轴上方的一个交点为P.
设点P的坐标为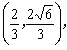求椭圆的方程；
在的条件下,经过点
的直线与抛物线交于若以线段为直径作圆,试判断抛物线的准线与椭圆的交点与圆的地方关系；
是不是存在实数
使得的边长是连续的自然数,的周长是6cm,且
若存在,求出如此的实数若没有,请说明理由。
21.有个首项为1,项数为的等差数列,设其第个等差数列的第项为
且公差为若
也成等差数列。
求的值,并求关于的表达式；
将数列分组如下:,设前组中所有数之和为求数列
的前项的和
设N是低于20的正整数,当
时,对于中的求使得不等式成立的所有N的值。
